Un equipo internacional revela una intrigante retroalimentación matemática que explica por qué las orillas de estos pétalos se curvan y terminan en puntas afiladas.

Pocas flores evocan tanto encanto como la rosa. Sin embargo, más allá de su intensa fragancia y elegante presencia, estas flores atesoran un hallazgo fascinante: un tipo de geometría “oculta” que moldea sus pétalos de manera inédita investigadores de distintas universidades, inspirados en una guía de floristerías de Hong Kong sobre patrones matemáticos, han determinado que los pétalos de rosa se rigen por algo más que la habitual secuencia de Fibonacci. El descubrimiento, publicado recientemente en la revista Science, revela una compatibilidad geométrica nunca antes vista que explica el característico borde ondulado de las rosas.

Físicos descubren insólita retroalimentación geométrica en los pétalos de rosa
El hallazgo surgió cuando un equipo de físicos, liderado por Zhang y respaldado por el especialista en morfogénesis Eran Sharon, se propuso descifrar por qué el crecimiento de los pétalos de rosa, a diferencia del de otras flores, presentaba picos y curvaturas llamativas en los bordes.

En primera instancia, comprobaron que la llamada “incompatibilidad de Gauss” un fenómeno ampliamente documentado en la formación de hojas y otros órganos vegetales no explicaba el perfil de las rosas. Por consiguiente, se aventuraron en la denominada incompatibilidad de Mainardi-Codazzi-Peterson, un mecanismo matemático prácticamente desconocido en la biología del crecimiento natural.

Análisis entre espirales florales y la inusual curva de la rosa
Muchos lectores se preguntarán: ¿cómo conectan los pétalos de rosa con conceptos como la sucesión de Fibonacci o la proporción áurea? La mayoría de flores ajustan su número de pétalos a las cifras de la secuencia de Fibonacci (3, 5, 8, 13, 21…), optimizando así la distribución de la luz y la atracción de polinizadores. Al mismo tiempo, otras especies exhiben espirales logarítmicas y ángulos dorados cercanos a 137,5°, garantizando una disposición perfecta.

No obstante, las rosas presentan una mecánica adicional: la tensión se concentra en los bordes, provocando cúspides localizadas y una curvatura más extrema. Esto resalta un tipo de “frustración geométrica” que, en última instancia, termina definiendo su silueta tan característica.

Tabla comparativa de pétalos y su número de Fibonacci
A continuación, se muestra una tabla con ejemplos de flores que siguen la secuencia de Fibonacci, en contraste con la rosa, que combina estos patrones con la nueva incompatibilidad descrita:

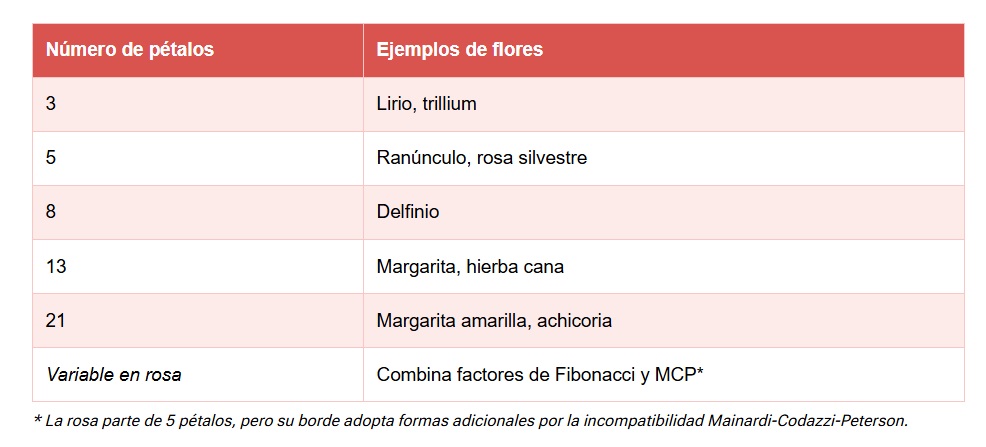
La rosa presenta un número de pétalos que suele estar entre 5 y un múltiplo de Fibonacci, pero su borde final adopta una forma que va más allá de la simple secuencia.

El papel de los fractales y la simetría en la floricultura

Aunque gran parte del reino vegetal exhibe fractales y simetría radial, la rosa reúne diversos rasgos en un solo pétalo. Por un lado, mantiene la simetría propia de las flores, y por otro, crea cúspides que surgen de la incompatibilidad MCP.

Este tipo de hallazgos podría tener implicaciones sorprendentes en ingeniería y arquitectura, donde los investigadores planean recrear estructuras autoajustables inspiradas en el “trucaje” geométrico de la rosa. De hecho, los diseños fractales ya se aplican en paneles solares, y las espirales logarítmicas sirven de modelo en antenas y sistemas de comunicación.

Lista con aplicaciones prácticas del descubrimiento

A continuación, se destacan algunos campos que se verán beneficiados:

• Biomimética: Mejora en la eficiencia de paneles fotovoltaicos basados en la distribución de pétalos.
• Diseño textil y arquitectura: Creación de materiales elásticos que se ondulan de forma controlada.
• Investigación biológica: Comprensión de cómo la tensión mecánica influye en la morfogénesis de las plantas.

Los especialistas señalan que estas conclusiones podrían extrapolarse a otras flores con bordes enérgicamente rizados, como ciertas variedades de orquídeas.

Un futuro repleto de rosas… y geometría

En consecuencia, esta revelación sobre la dinámica de los pétalos de rosa aporta una nueva perspectiva a la relación entre matemáticas y naturaleza. Al conjugar estudios teóricos, simulaciones por computadora y experimentos con láminas elásticas, el equipo de Zhang ha establecido un precedente en la forma de entender la morfogénesis vegetal.

¿La próxima meta? Ampliar la investigación a distintas familias florales y explorar si existen variaciones de la incompatibilidad de Mainardi-Codazzi-Peterson en otras especies. Por otro lado, ya se habla de exhibiciones donde los visitantes podrán apreciar réplicas de pétalos “sintéticos”, diseñados para ilustrar esta conexión íntima entre el crecimiento y la forma.

Este singular estudio no solo refuerza la relevancia de los patrones matemáticos en las flores, sino que añade un eslabón nunca antes observado: la geometría de los pétalos de rosa. Con los avances previstos en biomimética y la curiosidad de la comunidad científica al alza, todo apunta a que seguiremos encontrando nuevas sorpresas en la aparente sencillez de una flor.

El descubrimiento ha sido publicado recientemente y está disponible en la revista Science.